跳到主要内容

贝尔曼-福特算法

提示
  1. 贝尔曼-福特算法特点：贝尔曼-福特算法能处理带有负权重的边的图，并能检测负权重循环，避免了迪杰斯特拉算法无法处理负权重边的限制。
  2. 工作原理：通过迭代地放松所有顶点的估计路径长度，确保最终结果是最短路径。
  3. 算法应用：广泛应用于路由算法中计算最短路径，特别是在网络中寻找最短路径时，可以处理负权重边的情况。

它与 迪杰斯特拉算法 相似，但可以处理边的权重为负值的图。

为什么现实生活中会有边的权重为负？​

负权重边起初看似无用，但它们可以解释许多现象，如现金流、化学反应中的热量吸收/释放等。

例如，如果有多种方式从化学物质 A 变成化学物质 B，每种方法都会涉及吸热和放热的子反应。

如果我们想找到需要最少能量的反应集合，那么我们需要能够把热量吸收作为负权重，热量释放作为正权重来计算。

为什么我们需要对负权重小心？​

负权重边可以创建负权重循环，即一个通过回到同一点而减少总路径距离的循环。

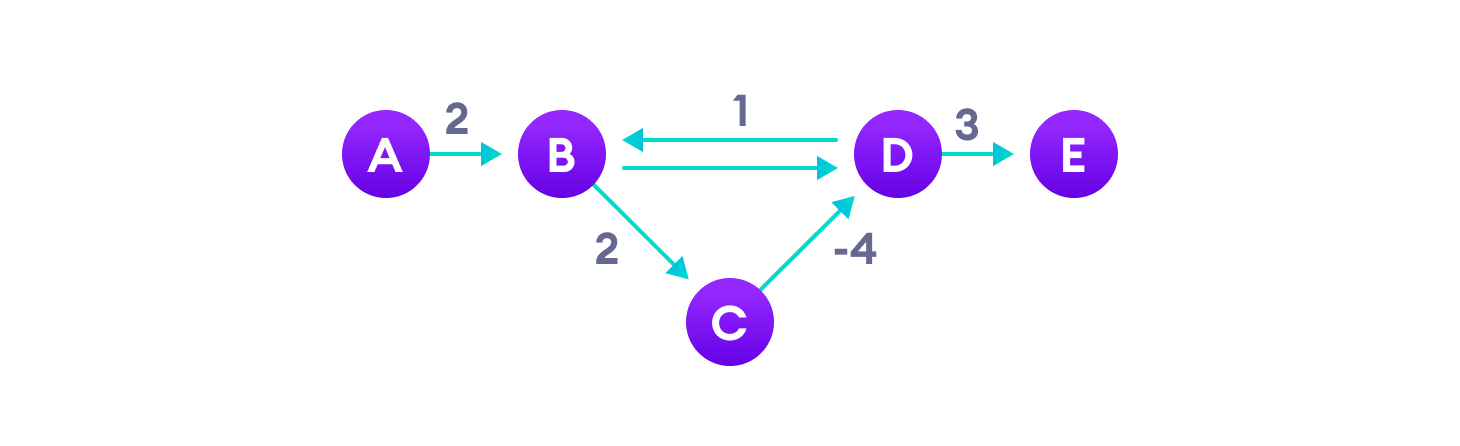
负权重循环在寻找最短路径时可能导致错误结果

像迪杰斯特拉算法这样的最短路径算法如果无法检测到这样的循环，可能会给出错误的结果，因为它们可能会通过一个负权重循环从而减少路径长度。

贝尔曼-福特算法的工作原理​

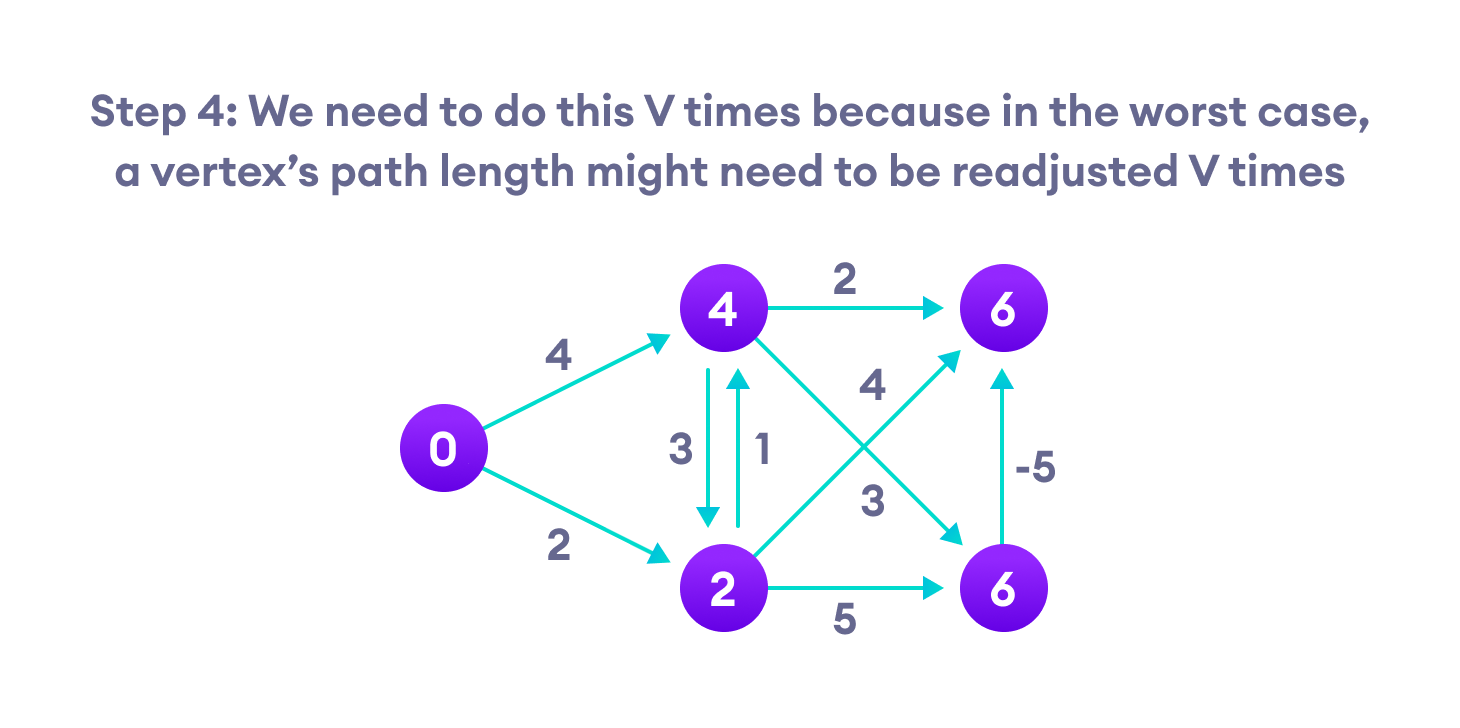
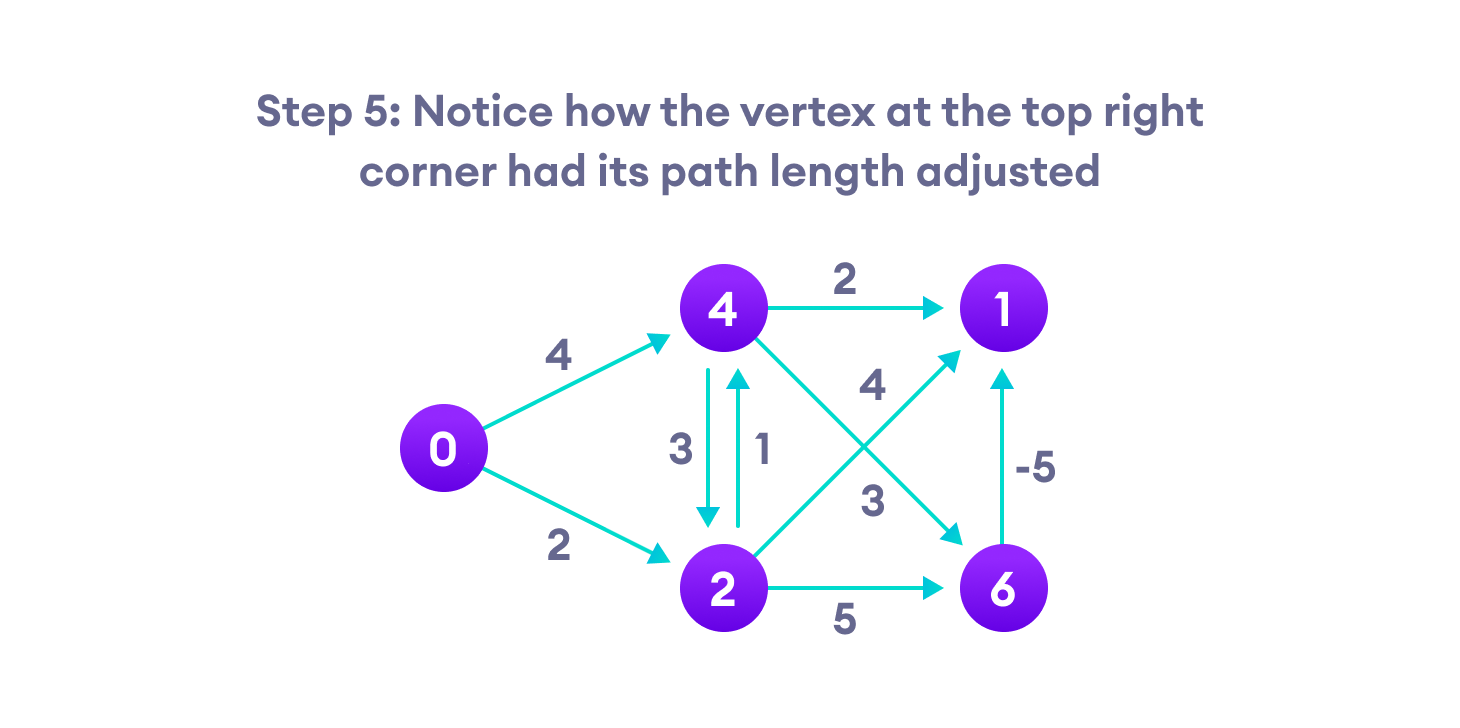
贝尔曼-福特算法通过对从起始顶点到所有其他顶点的路径长度进行高估来工作。然后它通过发现比之前高估的路径更短的新路径来迭代地放松这些估计。

通过对所有顶点重复这个过程，我们可以保证结果是优化的。

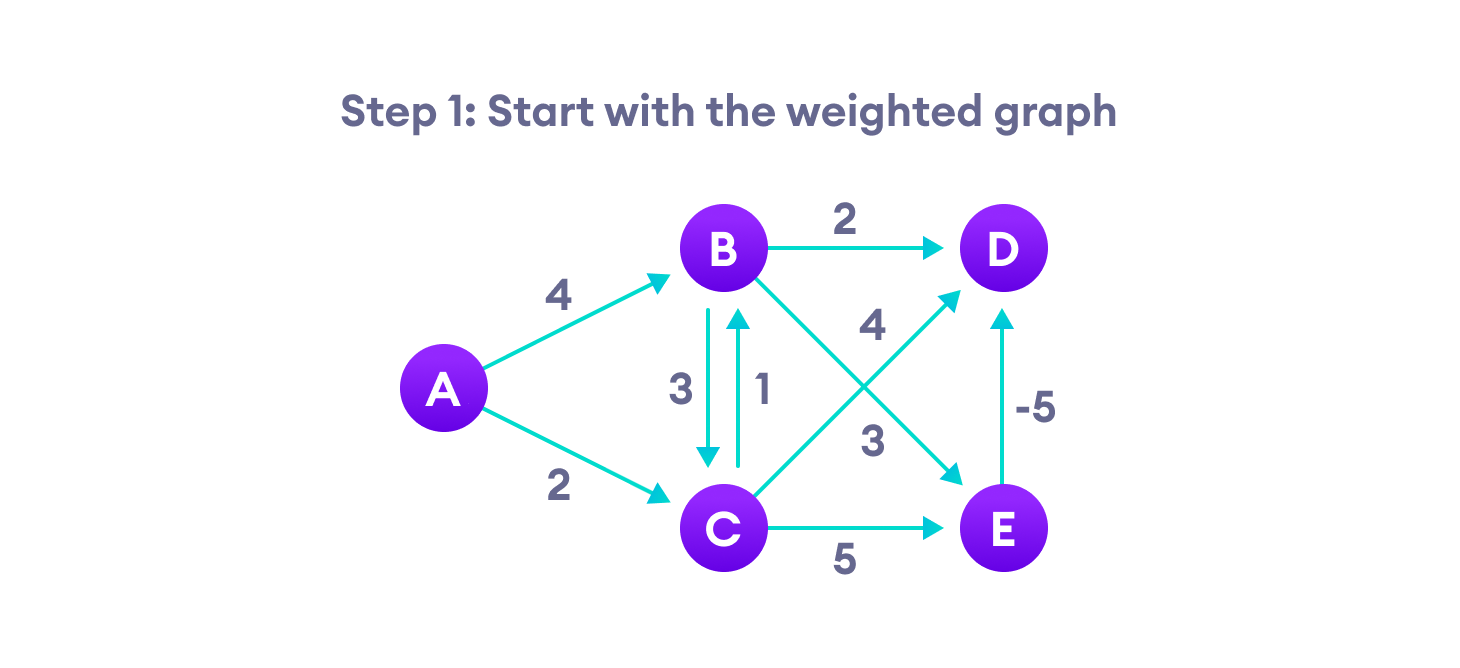
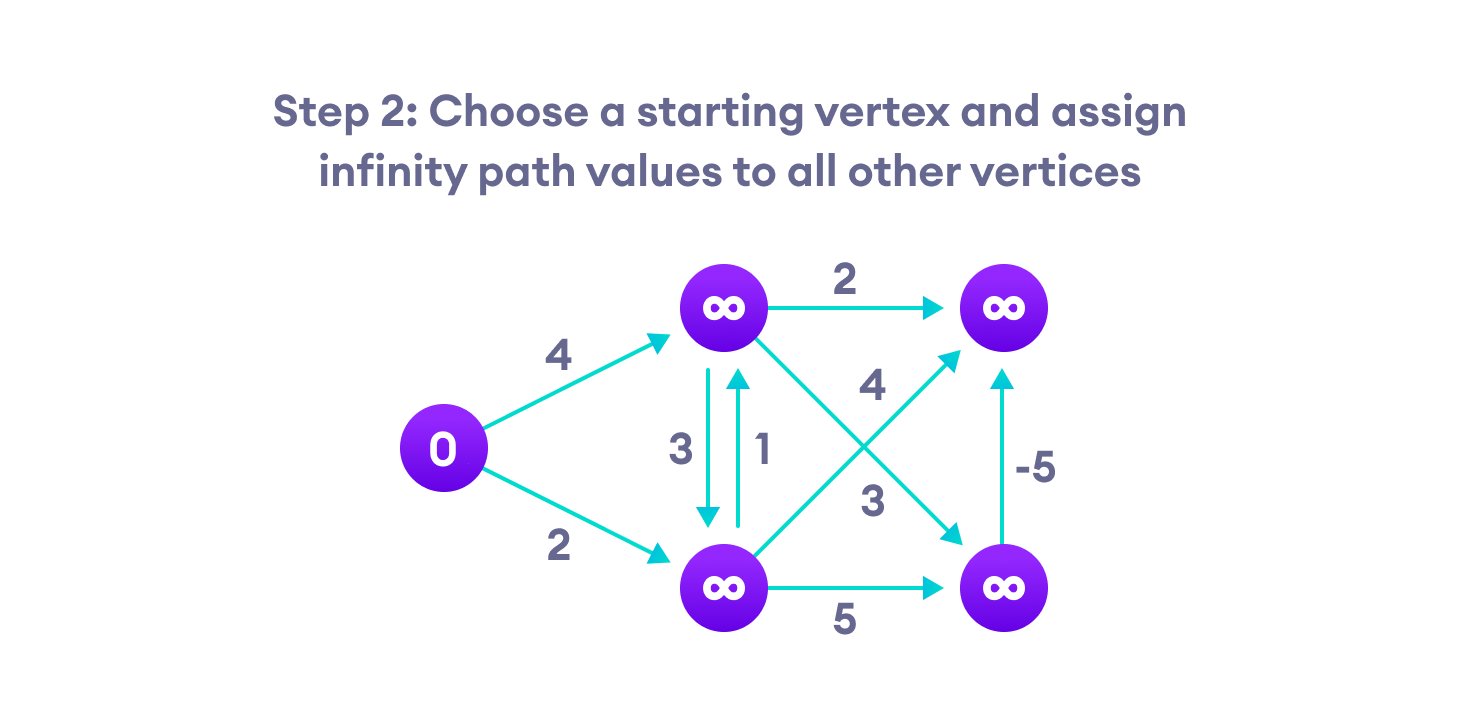
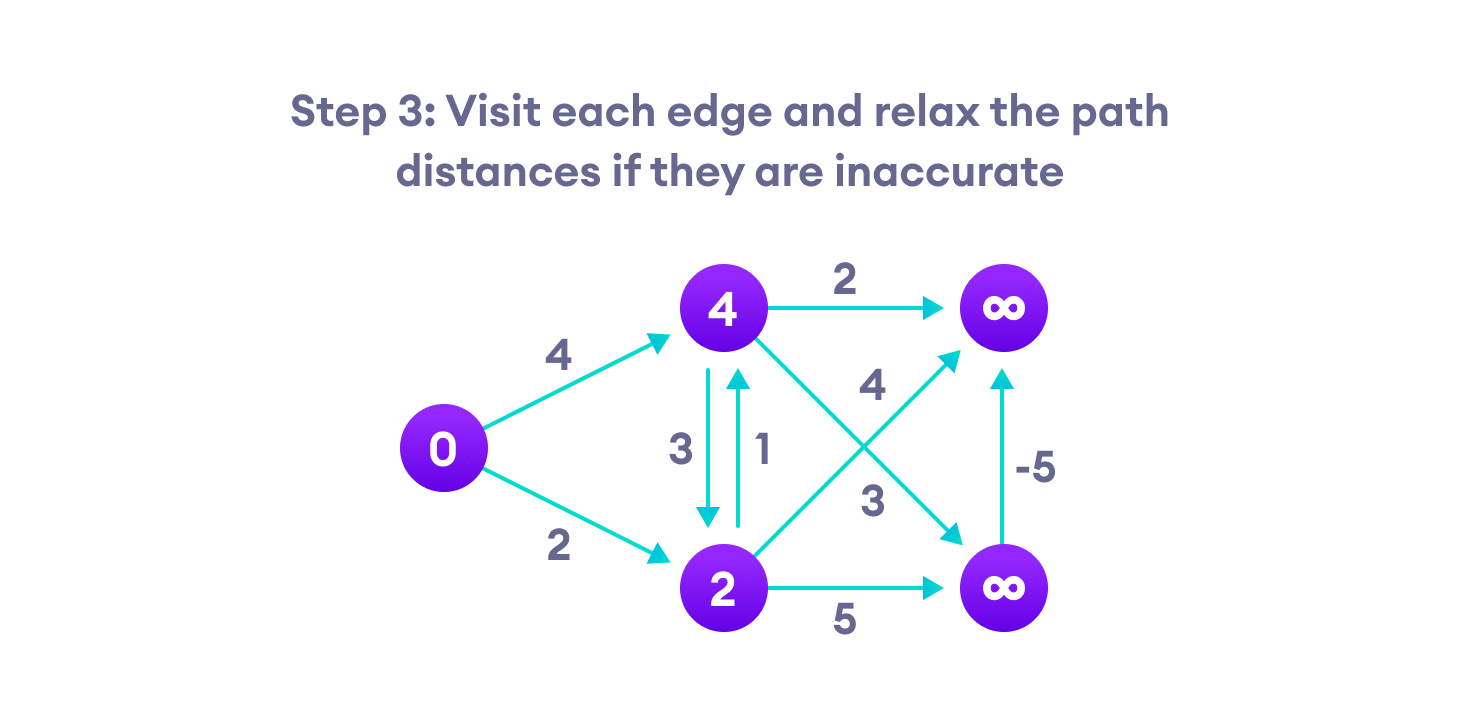
贝尔曼-福特算法的步骤

贝尔曼-福特算法的步骤

贝尔曼-福特算法的步骤

贝尔曼-福特算法的步骤

贝尔曼-福特算法的步骤

贝尔曼-福特算法的步骤

贝尔曼-福特伪代码​

我们需要维护每个顶点的路径距离。我们可以在一个大小为 v 的数组中存储它，其中 v 是顶点的数量。

我们还想能够得到最短路径，而不仅仅是知道最短路径的长度。为此，我们将每个顶点映射到最后更新其路径长度的顶点。

一旦算法结束，我们可以从目的顶点回溯到源顶点来找到路径。

function bellmanFord(G, S)
  for each vertex V in G
    distance[V] <- infinite
      previous[V] <- NULL
  distance[S] <- 0

  for each vertex V in G
    for each edge (U,V) in G
      tempDistance <- distance[U] + edge_weight(U, V)
      if tempDistance < distance[V]
        distance[V] <- tempDistance
        previous[V] <- U

  for each edge (U,V) in G
    if distance[U] + edge_weight(U, V) < distance[V}
      Error: Negative Cycle Exists

  return distance[], previous[]

贝尔曼-福特与迪杰斯特拉​

贝尔曼-福特算法和迪杰斯特拉算法在结构上非常相似。迪

杰斯特拉只关注一个顶点的直接邻居，而贝尔曼在每次迭代中都会遍历每条边。

迪杰斯特拉与贝尔曼-福特算法对比

Python、Java 和 C/C++ 示例​

Python Java C C++

# Python 中的贝尔曼-福特算法

class Graph:

    def __init__(self, vertices):
        self.V = vertices   # 图中顶点的总数
        self.graph = []     # 边的数组

    # 添加边
    def add_edge(self, s, d, w):
        self.graph.append([s, d, w])

    # 打印解决方案
    def print_solution(self, dist):
        print("顶点与源的距离")
        for i in range(self.V):
            print("{0}\t\t{1}".format(i, dist[i]))

    def bellman_ford(self, src):

        # 步骤 1: 填充距离数组和前驱数组
        dist = [float("Inf")] * self.V
        # 标记源顶点
        dist[src] = 0

        # 步骤 2: 放松边 |V| - 1 次
        for _ in range(self.V - 1):
            for s, d, w in self.graph:
                if dist[s] != float("Inf") and dist[s] + w < dist[d]:
                    dist[d] = dist[s] + w

        # 步骤 3: 检测负权重循环
        # 如果值发生变化，则我们的图中存在负权重循环
        # 我们无法找到最短距离
        for s, d, w in self.graph:
            if dist[s] != float("Inf") and dist[s] + w < dist[d]:
                print("图中包含负权重循环")
                return

        # 未发现负权重循环！
        # 打印距离和前驱数组
        self.print_solution(dist)

g = Graph(5)
g.add_edge(0, 1, 5)
g.add_edge(0, 2, 4)
g.add_edge(1, 3, 3)
g.add_edge(2, 1, 6)
g.add_edge(3, 2, 2)

g.bellman_ford(0)
// Java 中的贝尔曼-福特算法

class CreateGraph {

  // 创建图 - 它由边构成
  class CreateEdge {
    int s, d, w;

    CreateEdge() {
      s = d = w = 0;
    }
  };

  int V, E;
  CreateEdge edge[];

  // 创建一个具有 V 个顶点和 E 条边的图
  CreateGraph(int v, int e) {
    V = v;
    E = e;
    edge = new CreateEdge[e];
    for (int i = 0; i < e; ++i)
      edge[i] = new CreateEdge();
  }

  void BellmanFord(CreateGraph graph, int s) {
    int V = graph.V, E = graph.E;
    int dist[] = new int[V];

    // 步骤 1: 填充距离数组和前驱数组
    for (int i = 0; i < V; ++i)
      dist[i] = Integer.MAX_VALUE;

    // 标记源顶点
    dist[s] = 0;

    // 步骤 2: 放松边 |V| - 1 次
    for (int i = 1; i < V; ++i) {
      for (int j = 0; j < E; ++j) {
        // 获取边的数据
        int u = graph.edge[j].s;
        int v = graph.edge[j].d;
        int w = graph.edge[j].w;
        if (dist[u] != Integer.MAX_VALUE && dist[u] + w < dist[v])
          dist[v] = dist[u] + w;
      }
    }

    // 步骤 3: 检测负权环
    // 如果值改变，那么我们的图中有一个负权环
    // 我们无法找到最短距离
    for (int j = 0; j < E; ++j) {
      int u = graph.edge[j].s;
      int v = graph.edge[j].d;
      int w = graph.edge[j].w;
      if (dist[u] != Integer.MAX_VALUE && dist[u] + w < dist[v]) {
        System.out.println("CreateGraph 包含负权环");
        return;
      }
    }

    // 未找到负权环！
    // 打印距离和前驱数组
    printSolution(dist, V);
  }

  // 打印解决方案
  void printSolution(int dist[], int V) {
    System.out.println("顶点到源点的距离");
    for (int i = 0; i < V; ++i)
      System.out.println(i + "\t\t" + dist[i]);
  }

  public static void main(String[] args) {
    int V = 5; // 总顶点数
    int E = 8; // 总边数

    CreateGraph graph = new CreateGraph(V, E);

    // 边 0 --> 1
    graph.edge[0].s = 0;
    graph.edge[0].d = 1;
    graph.edge[0].w = 5;

    // 边 0 --> 2
    graph.edge[1].s = 0;
    graph.edge[1].d = 2;
    graph.edge[1].w = 4;

    // 边 1 --> 3
    graph.edge[2].s = 1;
    graph.edge[2].d = 3;
    graph.edge[2].w = 3;

    // 边 2 --> 1
    graph.edge[3].s = 2;
    graph.edge[3].d = 1;
    graph.edge[3].w = 6;

    // 边 3 --> 2
    graph.edge[4].s = 3;
    graph.edge[4].d = 2;
    graph.edge[4].w = 2;

    graph.BellmanFord(graph, 0); // 0 是源顶点
  }
}
// 在 C 中实现贝尔曼-福特算法

#include <stdio.h>
#include <stdlib.h>

#define INFINITY 99999

// 定义图的边的结构体
struct Edge {
  int u;  // 边的起始顶点
  int v;  // 边的结束顶点
  int w;  // 边的权重（u,v）
};

// 图 - 它由边组成
struct Graph {
  int V;        // 图中的顶点总数
  int E;        // 图中的边总数
  struct Edge *edge;  // 边的数组
};

void bellmanford(struct Graph *g, int source);
void display(int arr[], int size);

int main(void) {
  // 创建图
  struct Graph *g = (struct Graph *)malloc(sizeof(struct Graph));
  g->V = 4;  // 总顶点数
  g->E = 5;  // 总边数

  // 图的边数组
  g->edge = (struct Edge *)malloc(g->E * sizeof(struct Edge));

  // 添加图的边
  /*
		edge(u, v)
		其中	u = 边的起始顶点 (u,v)
				v = 边的结束顶点 (u,v)

		w 是边的权重 (u,v)
	*/

  // 边 0 --> 1
  g->edge[0].u = 0;
  g->edge[0].v = 1;
  g->edge[0].w = 5;

  // 边 0 --> 2
  g->edge[1].u = 0;
  g->edge[1].v = 2;
  g->edge[1].w = 4;

  // 边 1 --> 3
  g->edge[2].u = 1;
  g->edge[2].v = 3;
  g->edge[2].w = 3;

  // 边 2 --> 1
  g->edge[3].u = 2;
  g->edge[3].v = 1;
  g->edge[3].w = 6;

  // 边 3 --> 2
  g->edge[4].u = 3;
  g->edge[4].v = 2;
  g->edge[4].w = 2;

  bellmanford(g, 0);  // 0 是源顶点

  return 0;
}

void bellmanford(struct Graph *g, int source) {
  // 变量
  int i, j, u, v, w;

  // 图 g 的总顶点数
  int tV = g->V;

  // 图 g 的总边数
  int tE = g->E;

  // 距离数组
  // 大小等于图 g 的顶点数
  int d[tV];

  // 前驱数组
  // 大小等于图 g 的顶点数
  int p[tV];

  // 步骤 1: 填充距离数组和前驱数组
  for (i = 0; i < tV; i++) {
    d[i] = INFINITY;
    p[i] = 0;
  }

  // 标记源顶点
  d[source] = 0;

  // 步骤 2: 放松边 |V| - 1 次
  for (i = 1; i <= tV - 1; i++) {
    for (j = 0; j < tE; j++) {
      // 获取边的数据
      u = g->edge[j].u;
      v = g->edge[j].v;
      w = g->edge[j].w;

      if (d[u] != INFINITY && d[v] > d[u] + w) {
        d[v] = d[u] + w;
        p[v] = u;
      }
    }
  }

  // 步骤 3: 检测负权环
  // 如果值发生变化，表示我们的图中有一个负权环
  // 我们无法找到最短距离
  for (i = 0; i < tE; i++) {
    u = g->edge[i].u;
    v = g->edge[i].v

;
    w = g->edge[i].w;
    if (d[u] != INFINITY && d[v] > d[u] + w) {
      printf("检测到负权环！\n");
      return;
    }
  }

  // 未检测到负权环！
  // 打印距离和前驱数组
  printf("距离数组：");
  display(d, tV);
  printf("前驱数组：");
  display(p, tV);
}

void display(int arr[], int size) {
  int i;
  for (i = 0; i < size; i++) {
    printf("%d ", arr[i]);
  }
  printf("\n");
}
// C++ 中的贝尔曼-福特算法

#include <bits/stdc++.h>

// 图的边的结构体
struct Edge {
  int u;  // 边的起始顶点
  int v;  // 边的结束顶点
  int w;  // 边 (u,v) 的权重
};

// 图 - 它由边组成
struct Graph {
  int V;        // 图中顶点的总数
  int E;        // 图中边的总数
  struct Edge* edge;  // 边的数组
};

// 创建一个有 V 个顶点和 E 条边的图
struct Graph* createGraph(int V, int E) {
  struct Graph* graph = new Graph;
  graph->V = V;  // 总顶点数
  graph->E = E;  // 总边数

  // 图的边的数组
  graph->edge = new Edge[E];
  return graph;
}

// 打印解决方案
void printArr(int arr[], int size) {
  int i;
  for (i = 0; i < size; i++) {
    printf("%d ", arr[i]);
  }
  printf("\n");
}

void BellmanFord(struct Graph* graph, int u) {
  int V = graph->V;
  int E = graph->E;
  int dist[V];

  // 步骤 1: 填充距离数组和前驱数组
  for (int i = 0; i < V; i++)
    dist[i] = INT_MAX;

  // 标记源顶点
  dist[u] = 0;

  // 步骤 2: 放松边 |V| - 1 次
  for (int i = 1; i <= V - 1; i++) {
    for (int j = 0; j < E; j++) {
      // 获取边数据
      int u = graph->edge[j].u;
      int v = graph->edge[j].v;
      int w = graph->edge[j].w;
      if (dist[u] != INT_MAX && dist[u] + w < dist[v])
        dist[v] = dist[u] + w;
    }
  }

  // 步骤 3: 检测负权重循环
  // 如果值发生变化，则我们的图中存在负权重循环
  // 我们无法找到最短距离
  for (int i = 0; i < E; i++) {
    int u = graph->edge[i].u;
    int v = graph->edge[i].v;
    int w = graph->edge[i].w;
    if (dist[u] != INT_MAX && dist[u] + w < dist[v]) {
      printf("图中包含负权重循环");
      return;
    }
  }

  // 未发现负权重循环！
  // 打印距离和前驱数组
  printArr(dist, V);

  return;
}

int main() {
  // 创建一个图
  int V = 5;  // 总顶点数
  int E = 8;  // 总边数

  // 图的边的数组
  struct Graph* graph = createGraph(V, E);

  //------- 添加图的边
  /*
		edge(u, v)
		其中	u = 边 (u,v) 的起始顶点
				v = 边 (u,v) 的结束顶点

		w 是边 (u,v) 的权重
	*/

  // 边 0 --> 1
  graph->edge[0].u = 0;
  graph->edge[0].v = 1;
  graph->edge[0].w = 5;

  // 边 0 --> 2
  graph->edge[1].u = 0;
  graph->edge[1].v = 2;
  graph->edge[1].w = 4;

  // 边 1 --> 3
  graph->edge[2].u = 1;
  graph->edge[2].v = 3;
  graph->edge[2].w = 3;

  // 边 2 --> 1
  graph->edge[3].u = 2;
  graph->edge[3].v =1;
  graph->edge[3].w = 6;

  // 边 3 --> 2
  graph->edge[4].u = 3;
  graph->edge[4].v = 2;
  graph->edge[4].w = 2;

  BellmanFord(graph, 0);  // 0 是源顶点

  return 0;
}

贝尔曼-福特算法的复杂度​

时间复杂度​

| 最佳情况复杂度 | O(E) | | 平均情况复杂度 | O(VE) | | 最坏情况复杂度 | O(VE) |

空间复杂度​

空间复杂度为 O(V)。

贝尔曼-福特算法的应用​

  1. 用于路由算法中计算最短路径
  2. 用于寻找最短路径
最后于 更新